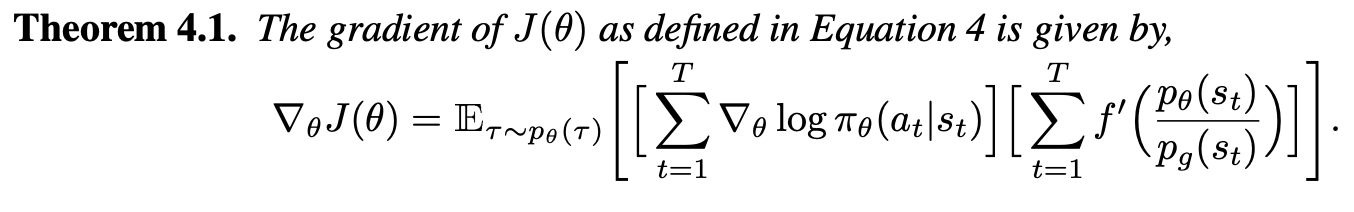
|
|
|
|
|
|
|
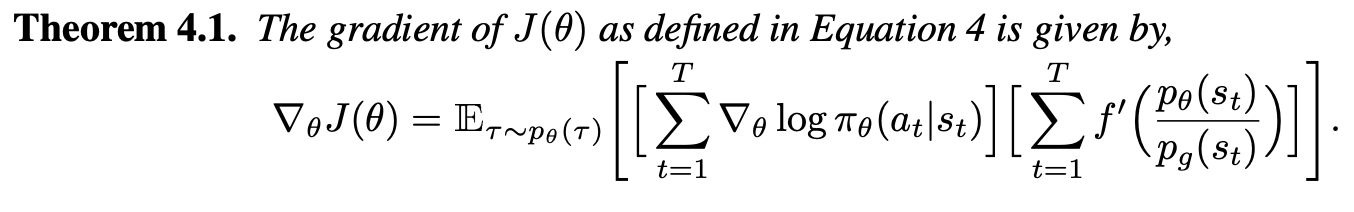
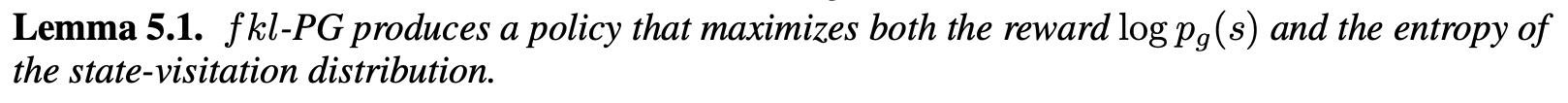

|

|
|
$f'\big(\frac{p_\theta(s)}{p_g(s)}\big)$ |
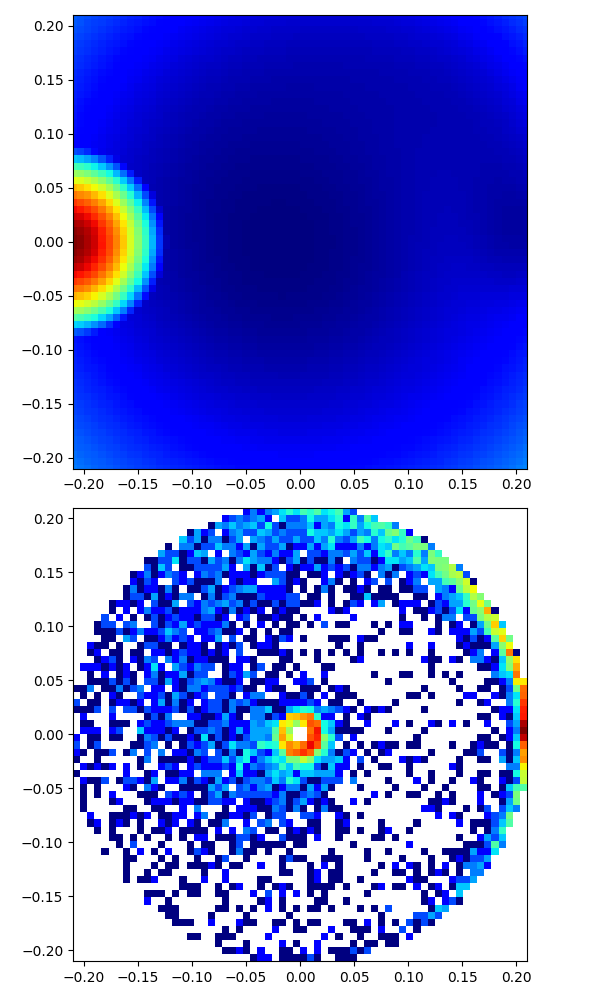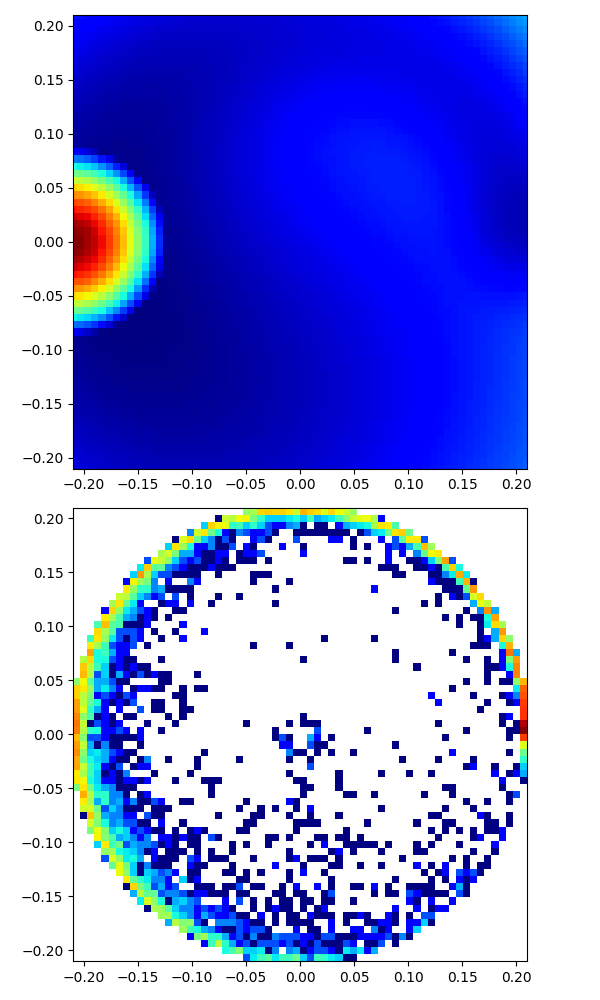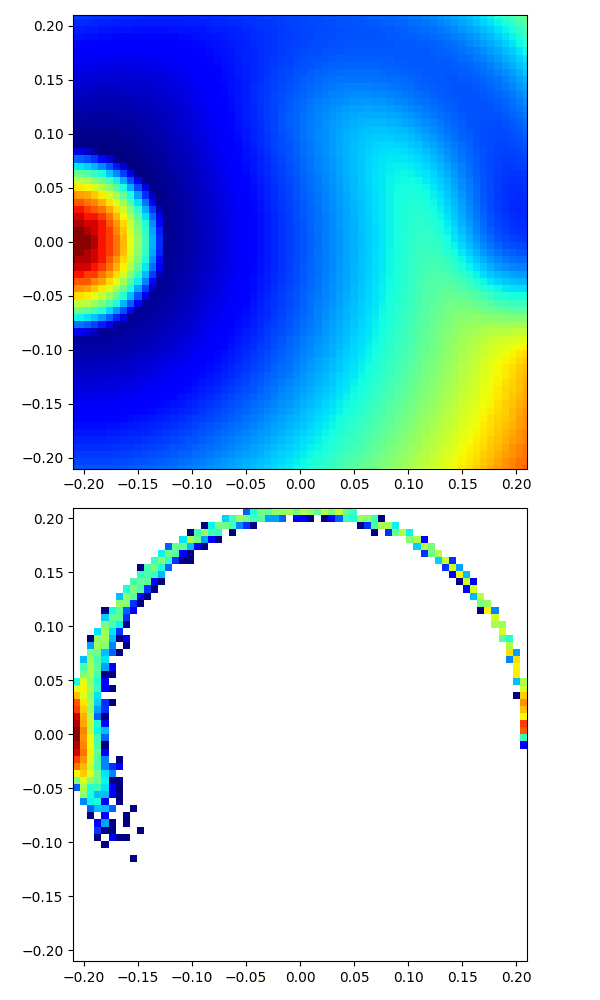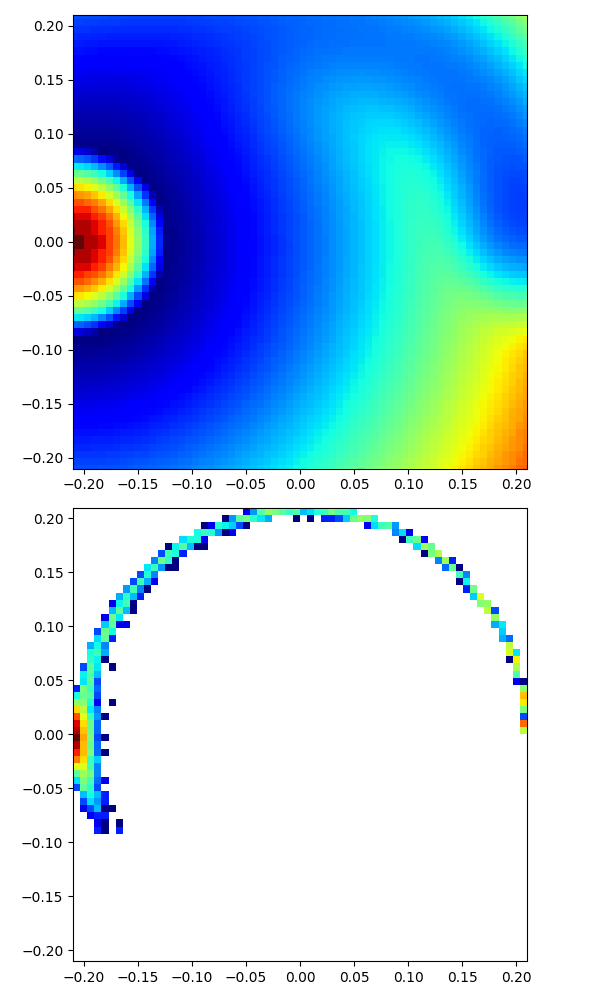
|
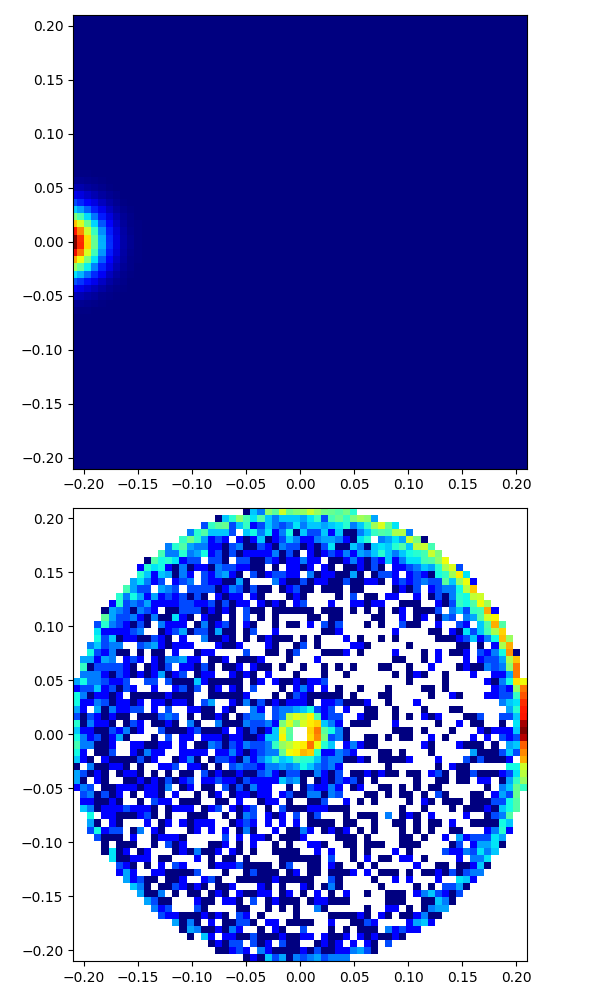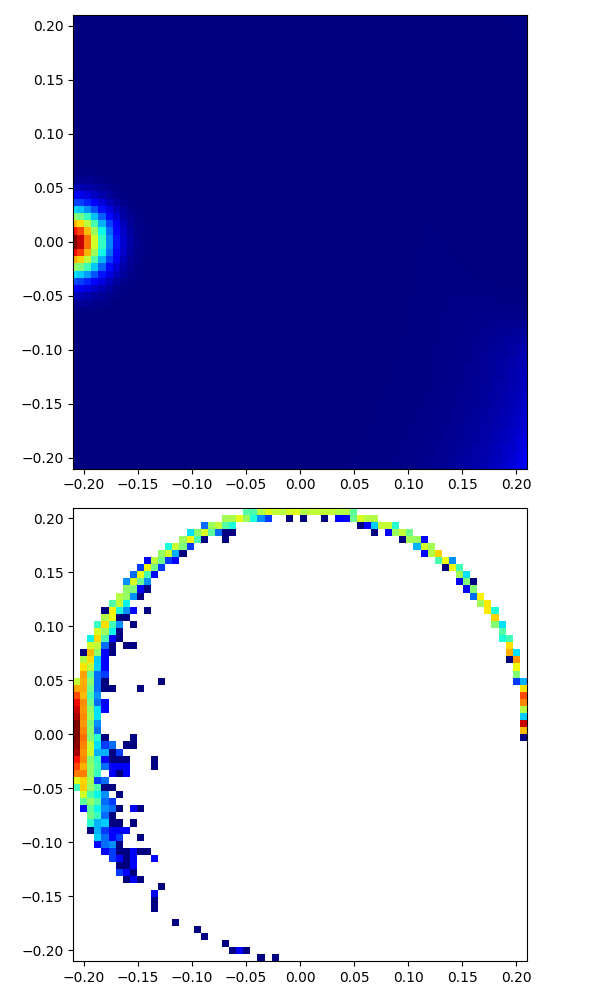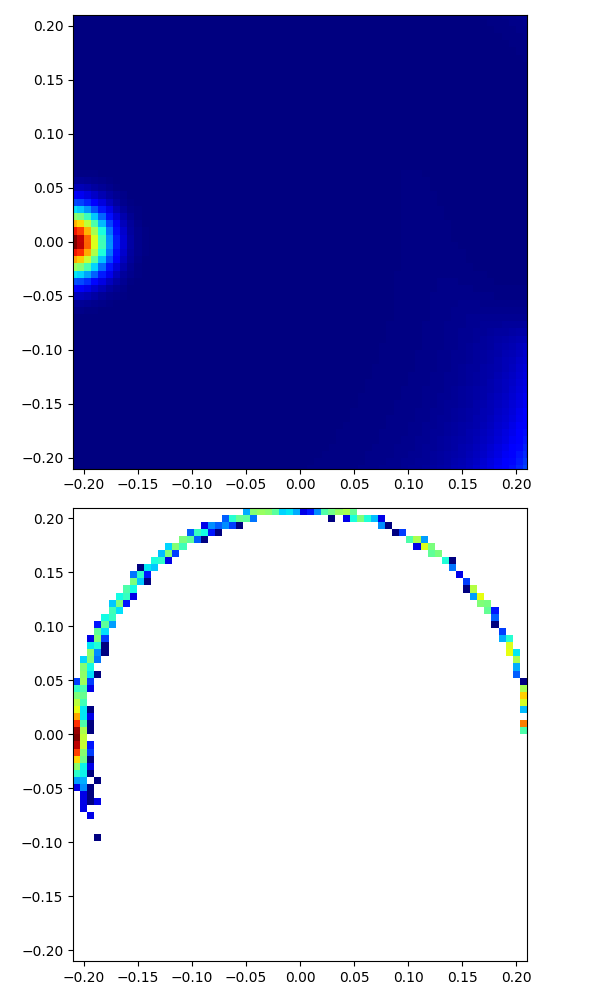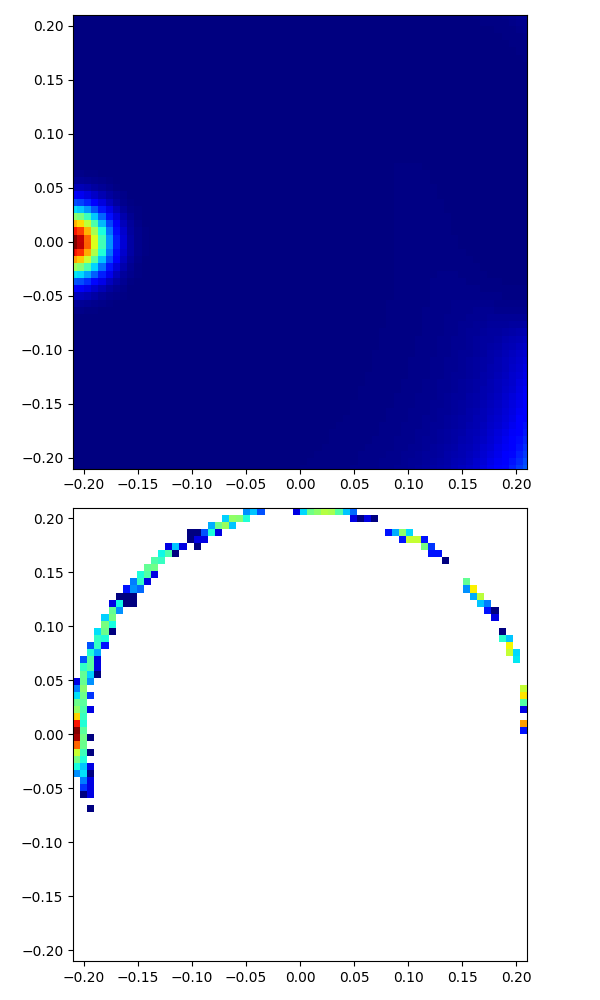
|
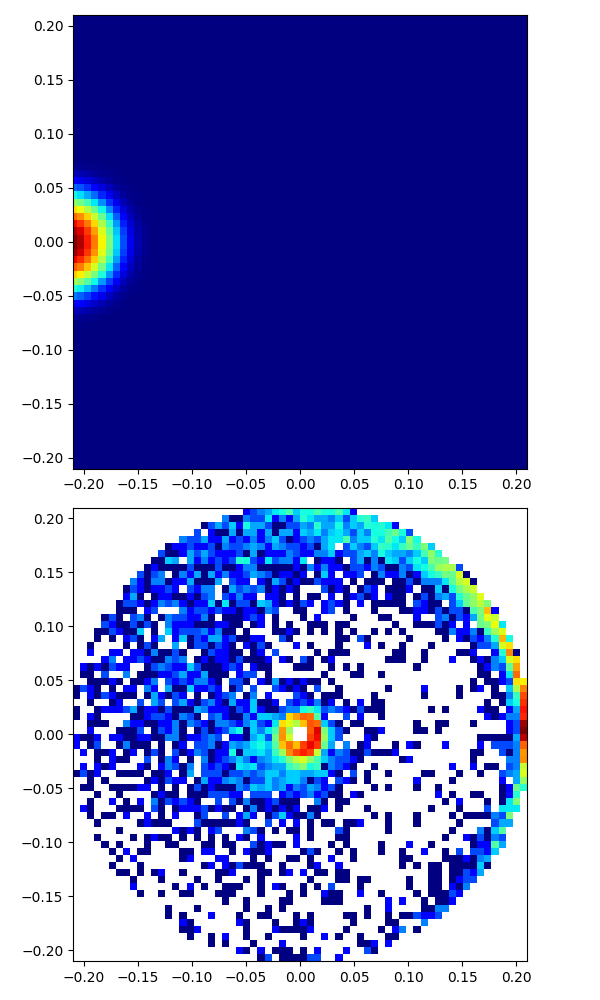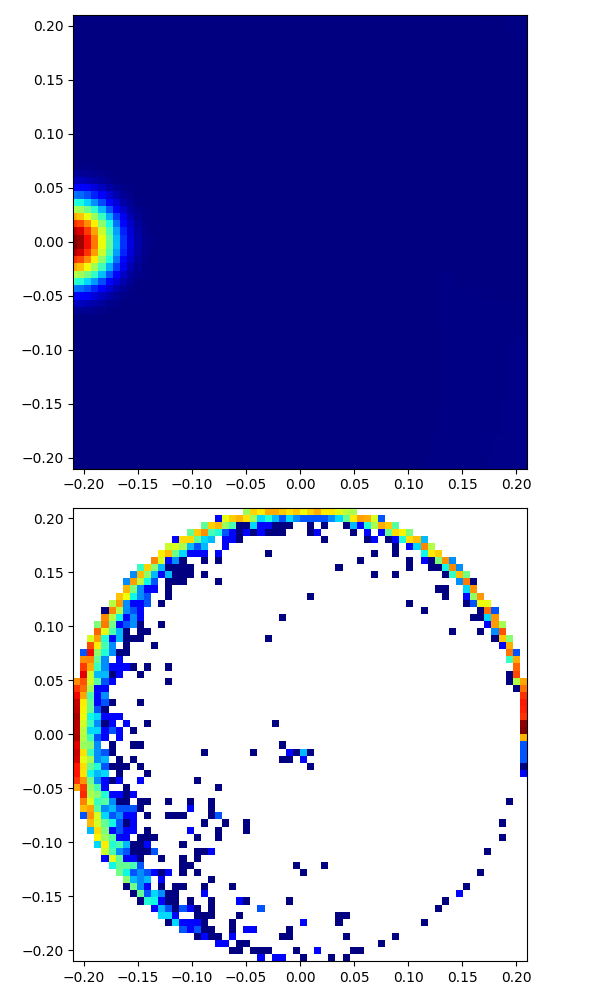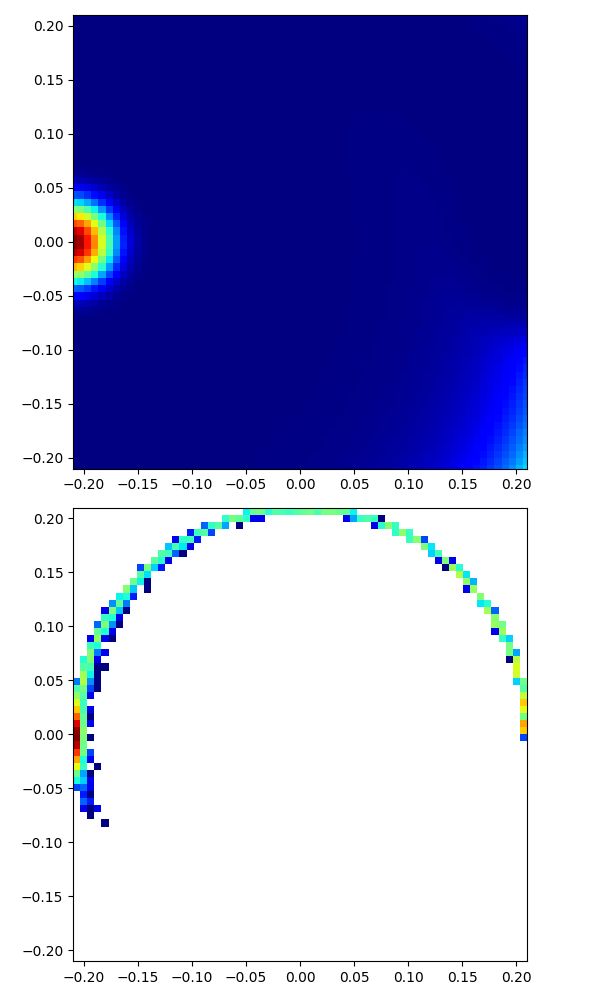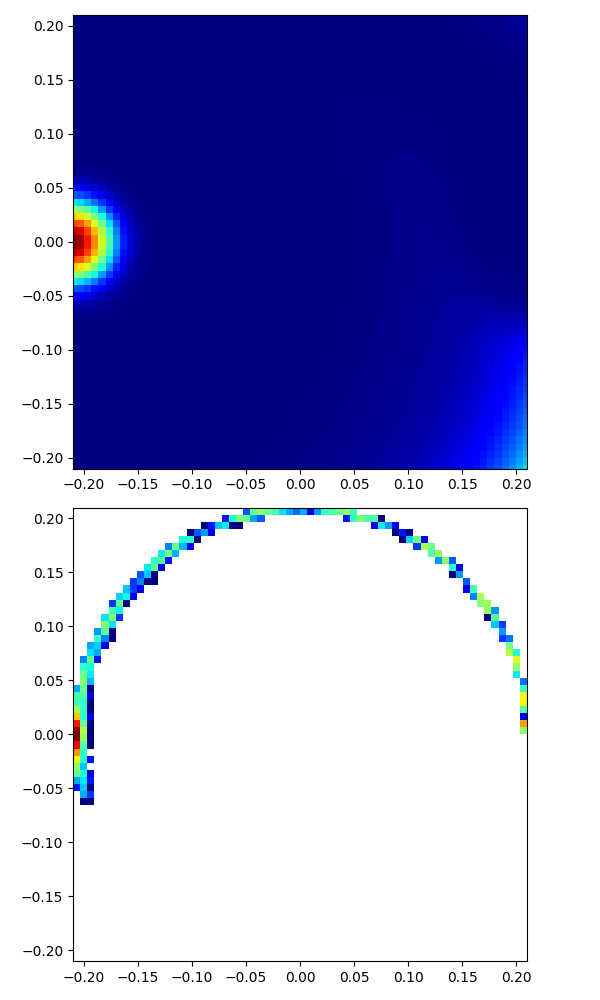
|
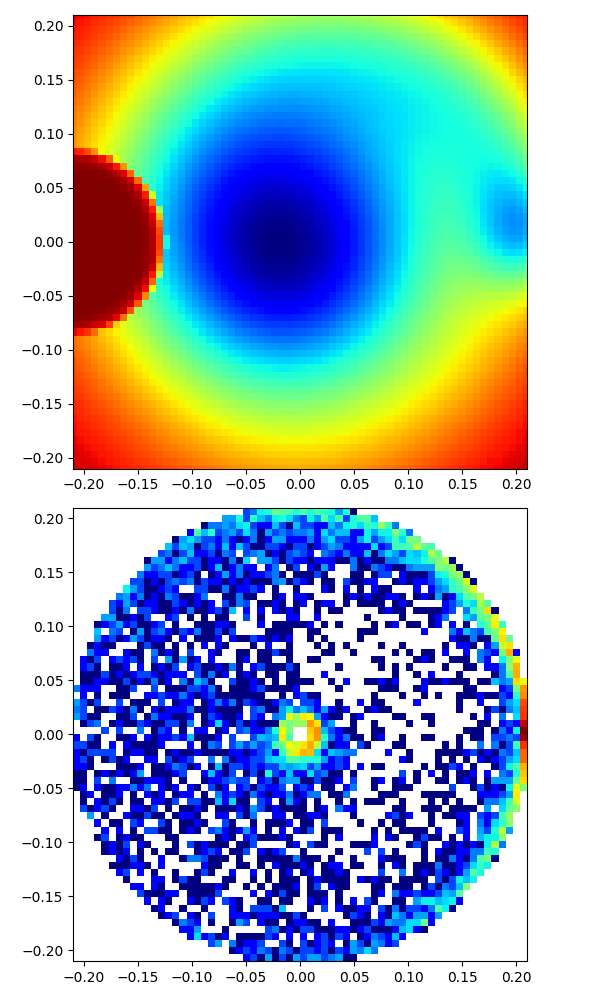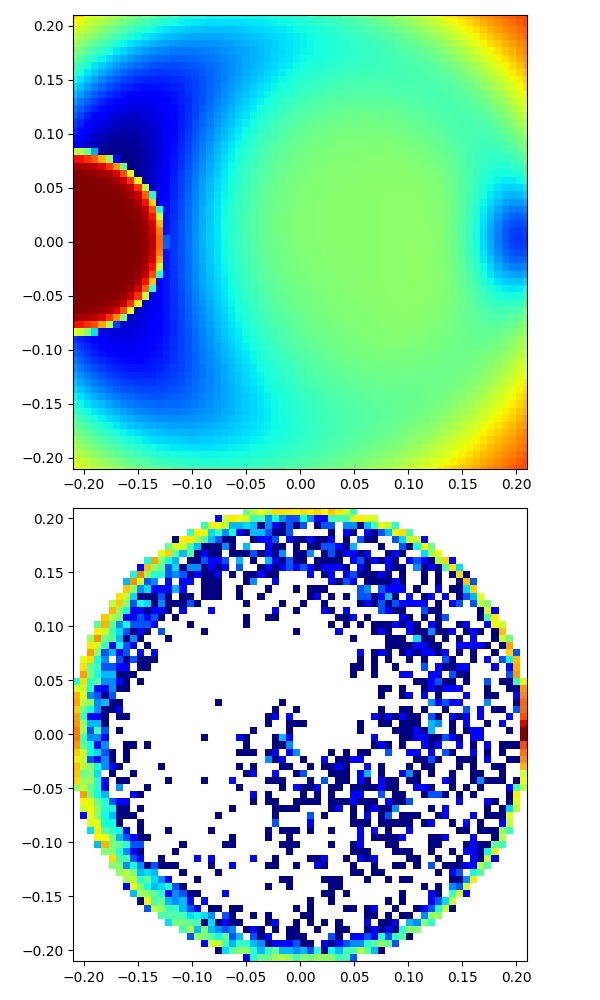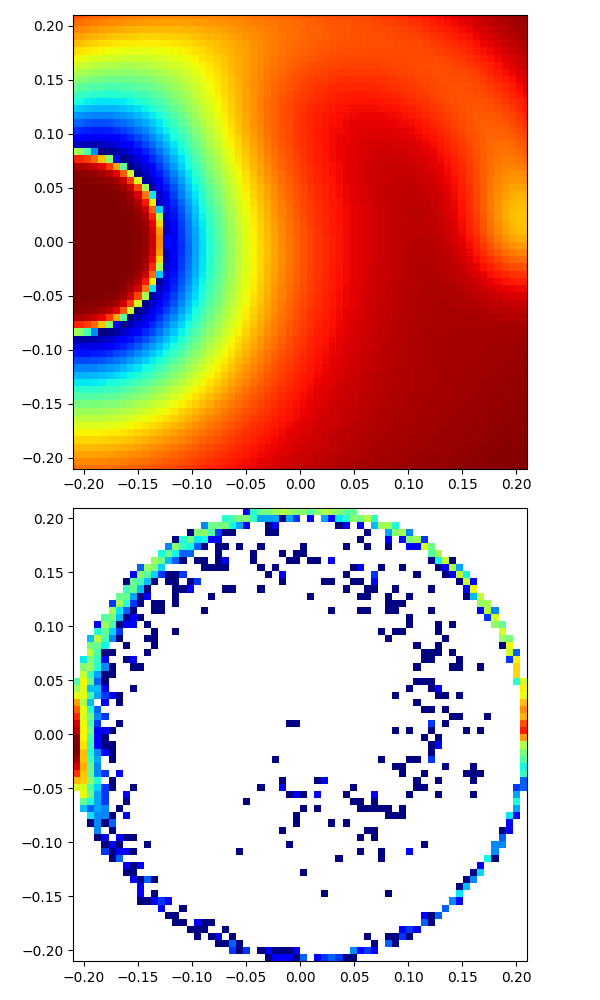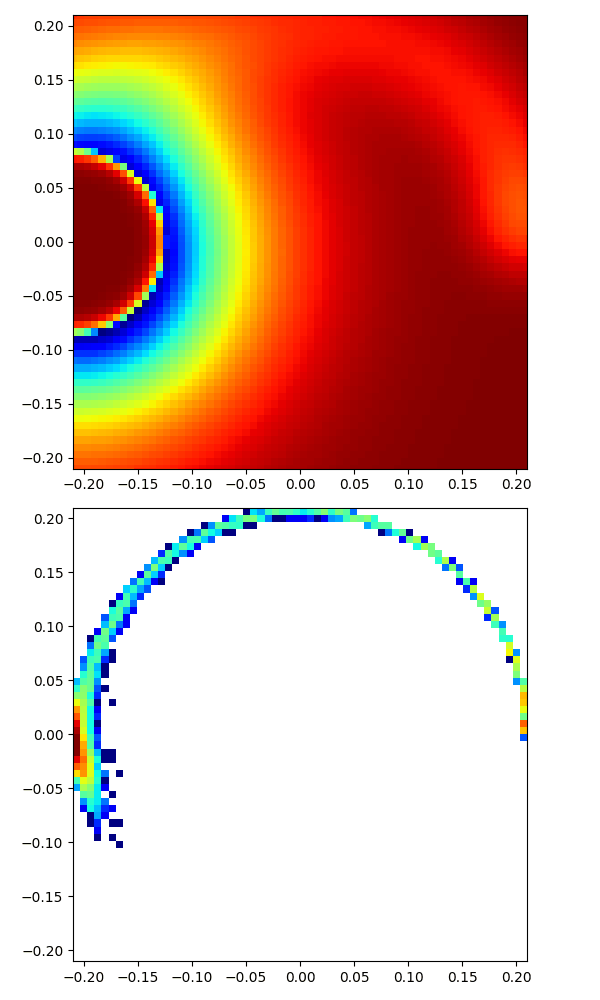
|
|
$p_\theta(s)$ |
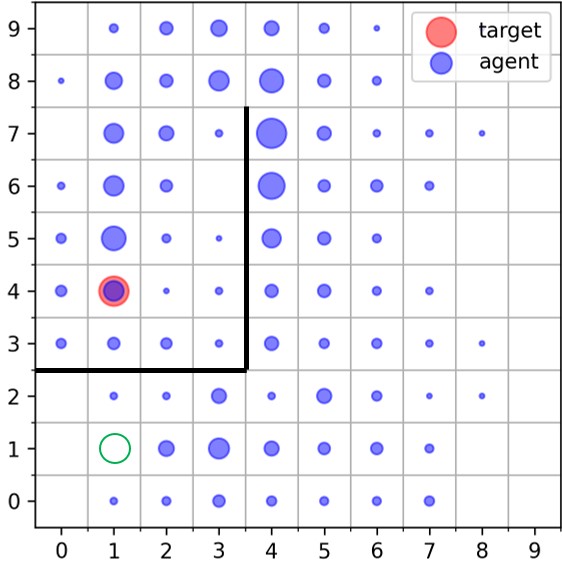
|
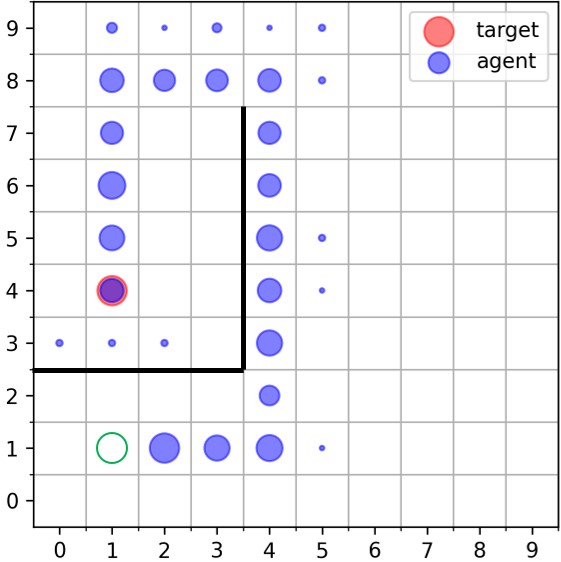
|
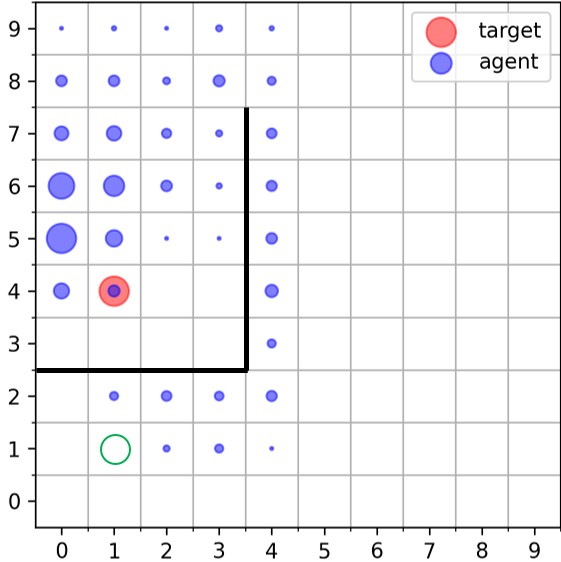
|
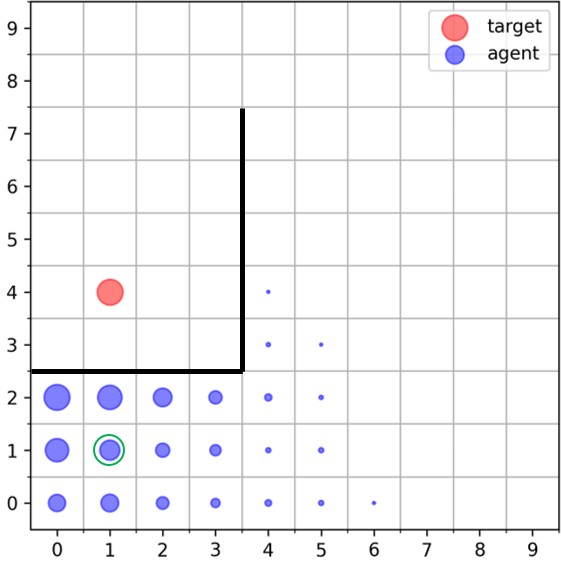
|
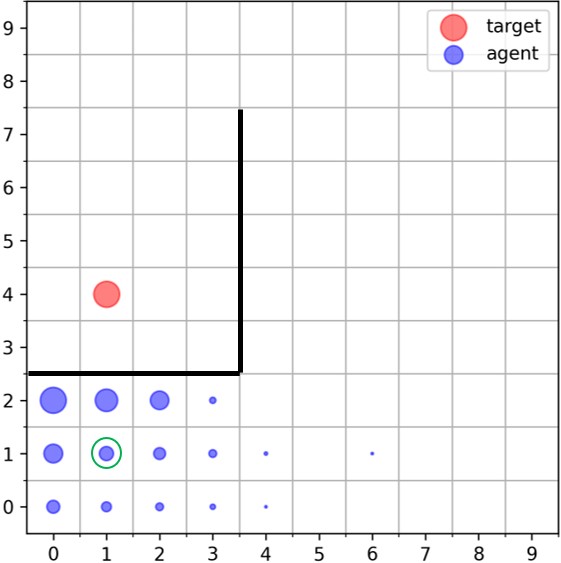
|
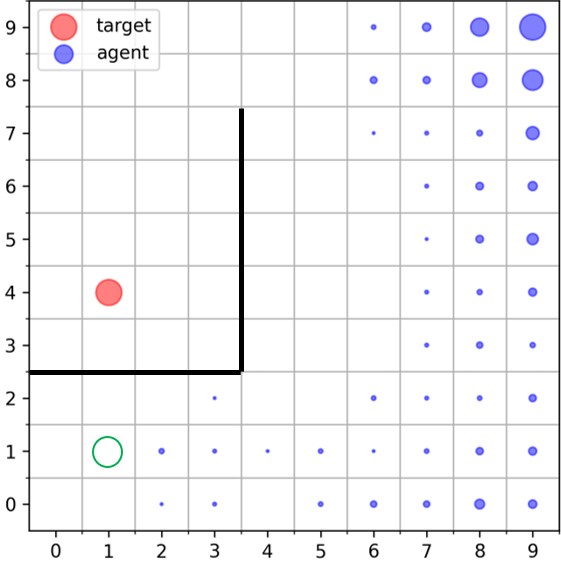
|
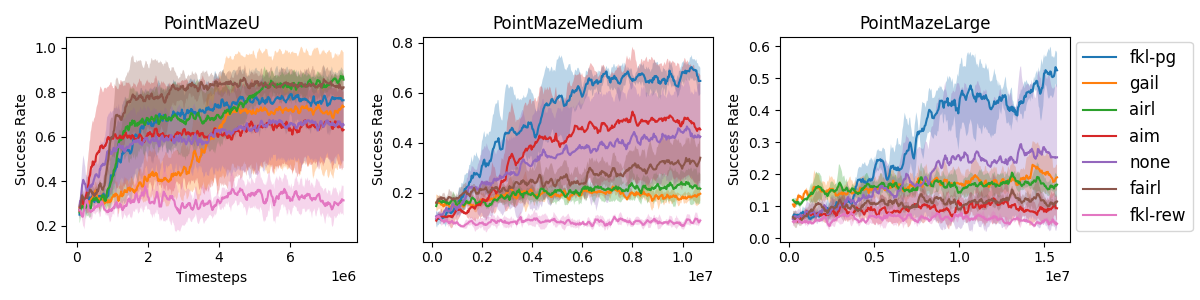
|
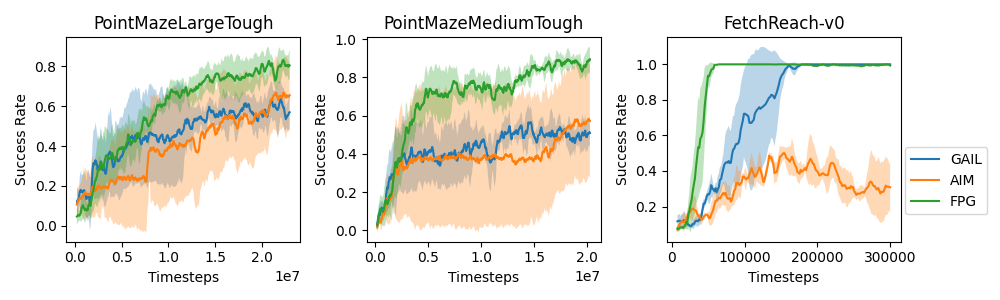
|
@inproceedings{agarwal2023fpg,
author = {Agarwal, Siddhant and Durugkar, Ishan and Stone, Peter and Zhang, Amy},
booktitle = {Advances in Neural Information Processing Systems},
title = {$f$ Policy Gradients: A General Framework for Goal Conditioned RL using $f$-Divergences},
volume = {36},
year = {2023}
}